Hey, friends today we are going to learn the basic fundamentals of structural analysis. Here, we will discuss about the calculation of the Kinematic indeterminacy and Static indeterminacy – Beam, Frame i.e static and kinematic concept and introduction.
So, to calculate the degree of indeterminacy of structure you must have to read and understand all the articles below step by step.
Why do we find the degree of indeterminacy of structure?
We find the degree of indeterminacy to check whether the structure is stable or unstable. There no worth of constructing any structure if it is not durable, Right?
Types of the degree of indeterminacy
- The degree of static indeterminacy (Ds)
- The degree of kinematic indeterminacy(Dk)
The Total indeterminacy of structure is given by the sum of the degree of static indeterminacy and kinematic indeterminacy.
Types of static indeterminacy (Ds)
- Internal static indeterminacy
- External total indeterminacy
The total static indeterminacy is given by the sum of external static indeterminacy (DSe) and internal static indeterminacy (DSi)
What is kinematic indeterminacy?
It is defined as the number of non-zero joints displacement of the structure. It is also called the Degree of freedom.
For better understand, I have made a chart summary of important formulae.

Where,
R= no. of unknown reaction
r=3 + (additional equation due to internal thing if any)
no. of available equation
M= no. of member
J= no. of joints
C= no. of closed loop
According to the above chart, we are going to calculate the degree of indeterminacy of beam, frame, and truss.
For each structure, there are the different formula of static and kinematic indeterminacy.
In the above table, I have marked with red color which you don’t have to remember or follow these formulae because in question it is given to neglect axial information.
But the third one for truss is very important for calculation. So, except marked formulae of beam and frame, all the formulae are important for calculation.
But how to calculate the degree of kinematic indeterminacy of beam and frame?
Yes, don’t worry I will explain all in the problem in which I have solved below. For basic knowledge to calculate degree if kinematic indeterminacy let us read the chart below.

Description of the above chart
- If there is a fixed end then there will not be any value of kinematic indeterminacy and tends to zero.
- In hinged support, dynamic indeterminacy will be one (1).
- In roller support, kinematic indeterminacy will be two (2) with axial deformation and one (1) if axial deformation is neglected.
- If there is an internal hinge with two members then dynamic indeterminacy will be two(2).
- If the internal hinge is with three members then dynamic indeterminacy will be three (3).
- For the free end, the dynamic indeterminacy will be two (2).
Numericals to calculate degree of indeterminancy of structure
Q) Find the degree of Kinematic indeterminacy and Static indeterminacy of the structure as shown in the figure.
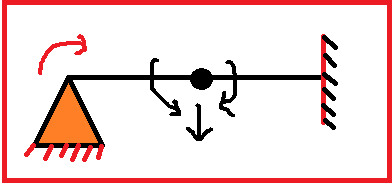
Solution,
We have,
Ds = DSe + DSi [ Let equation——(1)]
By formula,
DSe = (R-3) – (M’-1)
Since there is internal hinge,
We add M’ ( Number of member.)
So, DSe = (5-3) – (2-1)
Again, DSi = 0 For Beam
DS = 1+0 From equation —-(1)
= 1
and DK = 4
Hence,
Degree of Kinematic indeterminacy(DK) = 4
and Degree of Static indeterminacy(DS) = 1
Description of the above calculation
- In the above calculation at first equation of degree of static indeterminacy has written and given naming as equation -1.
- After that internal static indeterminacy has calculated (DSe).
- m’ stand for a number of members which is two in the above calculation, if there were three members at hinge then the value of m’ would be three (3).
- After that, the value of external static indeterminacy has calculated (DSe).
- Now to calculate the total degree of static indeterminacy internal and external static indeterminacy has added.
- At last value of kinematic indeterminacy has calculated. One support is hinge has one, and there is one hinge which has three kinematic indeterminacy. So, as a whole, its value is four (4).
Hence, in this way you can calculate the degree of indeterminacy of any structure.
Did you like? Please Share it !!!
Read Also,
Analysis- Conjugate beam method with Numerical Example
Minimum clear cover for slab, column, beam, Retaining Structure
Difference between Tie beam and Plinth beam – and their Function